2月度その6:気になるシリーズ :フラクタル⬅分かる、1/fゆらぎ⬅理解できる、でも何故1/fゆらぎがフラクタルなのか?が分からない!
気になるシリーズ:フラクタル⬅分かる、1/fゆらぎ⬅理解できる、でも何故1/fゆらぎがフラクタルなのか?が分からない!
この黒点サイトでは現在、「太陽黒点数の推移」「太陽黒点数とS&P500、VIXとの相関」「エルニーニョ南方振動ELSOと太陽黒点数との相関」の3タイプを月初に更新しています
しかしながら、ベッドで寝っ転がっていると漠然と頭に浮かんで来る疑問がありまして、それは私にとっての未解決問題もしくは気に掛かる問題なのです
かねてからフラクタルとは(それなりに)分かっているつもりで、1/fゆらぎも観測事実として(それなりに)理解しているつもりで、でも、何故1/fゆらぎがフラクタルであるのか?分からない!⬅ これが随分と前から分からなくて気に掛かっておりましたので、今回、追ってみました!
お付き合い頂ければ幸いです
まず [フラクタル - Wikipedia] から:
はい、部分と全体が自己相似(要するに、似ている)ですね? OKです
再帰とは、自分で自分を呼び出す(Callする)プログラム構造、の事です
例が挙げてあります:
フラクタルの具体的な例としては、海岸線の形が挙げられる。一般的な図形は複雑に入り組んだ形状をしていても、拡大するに従ってその細部は変化が少なくなり、滑らかな形状になっていく。これに対して海岸線は、どれだけ拡大しても同じように複雑に入り組んだ形状が現れる。
海岸線の形状、、、
そして海岸線の長さを測ろうとする場合、より小さい物差しで測れば測るほど大きな物差しでは無視されていた微細な凹凸が測定されるようになり、その測定値は長くなっていく。したがって、このような図形の長さは無限大であると考えられる。
うむ〜、分子の大きさより小さな物差しで測る事は出来ないが、考え方として無限大に到達する、という事ですね
生物事例が挙がっていて、
ロマネスコ・カリフラワー:

By Fk:フラクタル形態のつぼみが特徴のカリフラワー
そして、バーンズリーのシダ:

By Laug:イギリスの数学者バーンズリーによって記述された、シダを模した、数式により生成されたパターン、自己相関(再帰)図形の代表例
次に述べる1/fゆらぎは、皆様ご存知の通り、人が心地よさを感じる原因であり源泉なのだけれども、 私はカリフラワーを見てもシダを見ても心地よいと思った事は無い!
そして [1/fゆらぎ - Wikipedia] である:
1/fゆらぎとは、パワー(スペクトル密度)が周波数 f に反比例するゆらぎのこと
ピンクノイズはこの1/fゆらぎを持つノイズであり、1/fノイズとも呼ばれる。
1/fゆらぎを持つ、ピンクノイズ:

By en:User:Ktims:周波数が10倍ごとに10dB減衰している。
それに対し周波数依存しないノイズが、ホワイトノイズ:
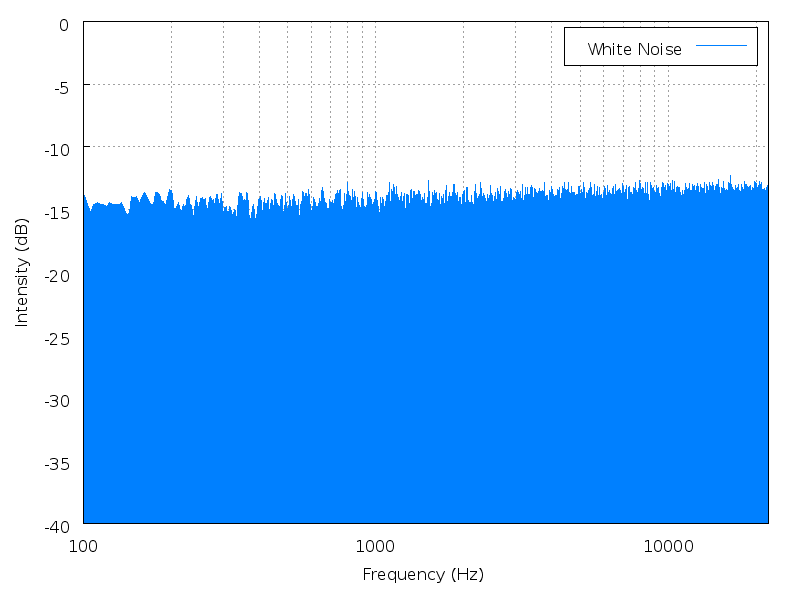
パブリック・ドメイン:ホワイトノイズに近似させ生成したノイズのパワースペクトラム
よく聞くノイズで表現するなら、「ザー」という音に聞こえる雑音がピンクノイズで、「シャー」と聞こえる音がホワイトノイズである。
ふむ、ザーとシャーですか、、、
ここで、1/fゆらぎに戻る:
1/fゆらぎは自然現象において見ることができ、具体例としては人の心拍の間隔、ろうそくの炎の揺れ方、電車の揺れ、小川のせせらぐ音、目の動き方、木漏れ日、蛍の光り方などがある。
ここで、「小川のせせらぐ音」や「電車の揺れ(眠くなる)」が心地よいのは確かである、1/fサウンドがかもし出す効果なのだろう、だが、それとフラクタルとはどのような関係があるのだろうか?が私の疑問なのである
「Wikiフラクタル」には、フラクタルは、1/fゆらぎに現れる
とか
「Wiki1/fゆらぎ」には、1/fゆらぎは、フラクタルな振動である
とか、記載されていないのである!
そこで、もう少し検索してみたら、
生体の1/fゆらぎとその解析法
[https://www.jstage.jst.go.jp/article/jsmbe1987/8/10/8_10_5/_pdf]
なる論文pdfを見つけた
東京大学教育学部の野崎大地さんと山本義春さんの論文で、1994年のBMEの論文である(BMEは日本生体医工学会の事で、私はこの学問・学会を知らなかった)
そこの図5に:

図5:1/f(β=1の場合の)ゆらぎがもつ自己相似(自己アフィン)な性質、下図の変動は上図の変動の一部を拡大したもの. 拡大しても変動の様相は変化しない.
なる図と説明が出て来る
論文では1/fのfは、右肩に指数βを持ち、β=1がピンクノイズであり上図はβ=1のピンクノイズの時系列信号(ちなみにβ=0がホワイトノイズ)なのである
自己相似(自己アフィン)とは、部分は全体と同じ形をしている、という事、要するに海岸線の事であり、シダの事であり、フラクタルである
従って、1/fゆらぎとは、fの右肩の指数βが1の場合であって、これをピンクノイズと言い、この場合にはフラクラル特性が包含されている、となる
しかし、あらゆるフラクタル特性が1/f(β=1)周波数特性をもたらすか?(ピンクノイズになるか?)という疑問が生ずる
又、あらゆる1/f(β=1)ゆらぎが心地よいサウンドになるのか?というと、恐らくそれは違うだろう
まとめさせて頂くと:
1.フラクタルとは、部分が全体と同じ形状をしている繰返し構造や特性を言う、構造の例としては海岸線やシダがある
2.1/f(fの指数β=1)ゆらぎとは、周波数成分の強度が周波数に反比例して弱くなる特性を持つゆらぎもしくはノイズの事で、ピンクノイズと称され、例として、小川のせせらぎ、や、電車の振動(確かに眠くなる!)がある
3.ここでピンクノイズは時系列信号を拡大すると、部分は全体と同じ形をしている(即ちフラクタル特性を持っている)観測事実がある ⬅ 私の疑問は、ひとまずこれで解決、だが次なる疑問は出てくる!(但し、ピンクノイズは数式で作っているので、原因は分かっているのだろう、私は現時点ではそこまで読み切れていない!)
4.しかし、あらゆるピンクノイズがフラクラル特性を持っているとして、あらゆるピンクノイズが心地よさをもたらすか?というと、恐らく、それは違う
一方、フラクタルは、図形としての繰返し構造と、時系列信号としての繰返し特性と、ふたつの自然界における事象に存在している
図形として見ていての心地よさ、と、時系列信号として聞いていて(もしくは揺られていて)の心地よさ、これは何が同じで、何が違うのか、を解析する必要があるだろう(既に解析済みで、私が知らないだけかもしれませんが)
以上、お付き合い頂き、誠にありがとう御座いました
感謝です